Primena binarnog stabla u igri IKS OKS

Binarno stablo (engl. binary tree) je u informatici struktura namenjena čuvanju podataka. Njene memorijske jedinice su organizovane po principu piramide. Tačnije, svaka memorijska jedinica (čvor) binarnog stabla može da pokazuje na još najviše dva elementa (njegova deca), dok stablo ima samo jedan elemenat na koga ne pokazuje ni jedan drugi (koren). Od ovog elementa se može doći u bilo koji drugi elemenat stabla. Svaki elemenat stabla može biti i svestan koji elemenat pokazuje na njega (tj. ko mu je roditelj).

Jedan od načina programiranja računara koji treba da pobedi u igri “iks-oks“, jeste rasporedjivanje mogućih poteza u binarno stablo. Svaka grana predstavlja po jedan potez, na primer, ta grana se se razgranava u tri različita pravca, jer je prvi u mogućnosti da odigra tri različita poteza.

1. Može staviti kružić u središnji kvadratić
2. Može ga staviti u ugao
3. Može ga staviti na kraj mreže

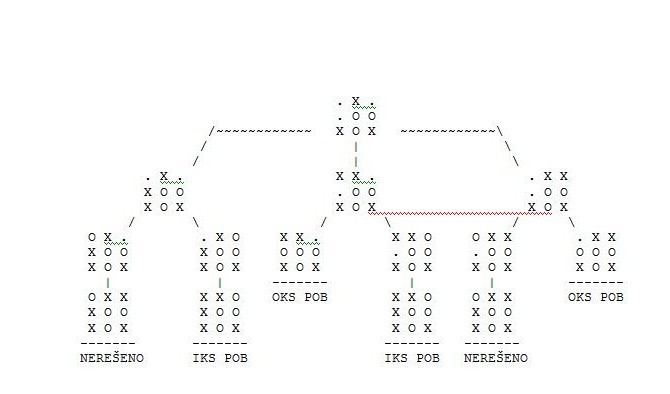
Zavisno od onoga što je napravio prvi igrač, drugi igrač, odnosno računar ima na raspolaganju tri ili pet poteza. Iz toga proizilazi da na drugom nivou ima ukupno 12 grana, a kako igra ide dalje, drvo se razvija, da bi na kraju doseglo broj od 500 grana. To je broj koji za računar ne predstavlja nikakav problem.

Stablo koja se odnosi na kraj stabla je prikazano u galeriji.

Isti pristup možemo upotrebiti u partiji šaha kako bismo utvrdili najbolju strategiju za pobedu. Još 1960. Godine je kompjuterski stručnjak, dr. Artur Samuel procenio da bi kompletno šahovsko stablo imalo deset na stotinu dvadeset ili 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 mogućih poteza.

Pošto je u pitanju jako puno poteza, računar, kako bi brže izvršio simulaciju vrši sečenje grana. I bira na desetine mogucih poteza unapred. Time zadaje problem igraču i stavlja ga u poziciju da izgubi partiju.